McCullogh-Pitts Neuron

Introduction

Credits

---

Theory

The first computational model for an artificial neuron was proposed by McCulloch and Pitts in 1943. The main difference between this model and the Artificial Neuron model is the use of absolute inhibitory input. This neuron is able to implement nonmonotonic logic functions.

The inputs and outputs are binary (exclusively ones or zeros); the nodes produce only binary results. There are no weights, and the activation function is always the unit step function. Thus, the elements of a McCulloch-Pitts neuron are

1. A set of n excitatory inputs, x_i.
2. A set of m inhibitory inputs, x_n+j
3. A threshold, u.
4. A unit step activation function.
5. A single neuron output, y.

In diagrams, we can represent a McCulloch-Pitts neuron as a circle labeled with the threshold value;  inhibitory inputs are indicated with a small circle, as shown below.

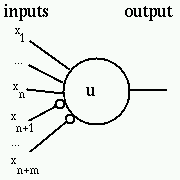
McCulloch-Pitts neurons have some nice theoretical properties:

• one can construct constant-delay circuits with them
• because they use threshold logic, component replication can be used to achieve fault tolerance -- both in the case of unreliable computing units, and of unreliable connetions.

Applet

• To change the inputs, click on the buttons.
• To change the threshold, type a new value in the field inside the circle and press the RETURN key.
• Important! To toggle an input from excitatory to inhibitory, click on the arrowhead. The arrowhead changes to a dot. To change back, click again.

Questions

1. Which of the 2-input binary logical functions can be computed with a McCulloch-Pitts
• neuron?
• network?
2. We can define two kinds of inhibition:
• relative inhibition, the kind used in an Artificial Neuron with a unit step function, is implemented using negative weights
• absolute inhibition, the kind used in McCulloch-Pitts units.
Convince yourself that networks of McCulloch-Pitts units are equivalent to networks with relative inhibition.  (A unit in a relative inhibition network has an "equivalent circuit" composed of one or more absolute inhibition units.)
3. [Optional paper and pencil problem] So far we have neglected time.  Let us introduce discrete time by specifying that each unit updates its output in one time step.  Thus if an input arrives at time t, the result is updated at t+1.  This allows us to build recurrent networks and is more biologically plausible.

With this modification it can be shown that any finite automaton can be simulated with a network of McCulloch-Pitts units.  (An automaton is a device that assumes different states; at any time step, the next state is determined by the current state and the current input. The state transitions and output of an automaton may be represented in a state transition table and output table or in a state transition diagram.)
Design a recurrent McCulloch-Pitts network to add two sequential streams of bits.