

Sig: Práctica: Suma de Prefijos Sup: La Función pipe Ant: Comunicaciones Entre Todos los
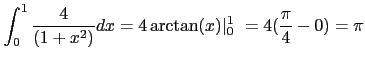
Esta integral puede aproximarse por la suma:
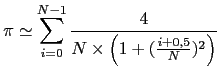 |
(4.1) |
Escriba un programa Perl que calcule ![]() usando varios procesos
cada uno de los cuales calcula una parte de la suma
asociada con la integral anterior.
Haga uso de la función
usando varios procesos
cada uno de los cuales calcula una parte de la suma
asociada con la integral anterior.
Haga uso de la función pipe (sección 4.1).
Si necesita hacer uso del depurador repase la
sección 3.3).
Casiano Rodríguez León
