

Sig: Práctica: Paralelismo de Granja Sup: Comunicación Bidireccional con Open2 Ant: Un Ejemplo con Lecturas
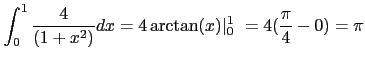 |
y usando comunicaciones bidireccionales usando manejadores
abiertos con open2
escriba una nueva versión distribuida del cálculo de ![]() .
Una posible versión en C++ es la siguiente:
.
Una posible versión en C++ es la siguiente:
#include <iostream>
using namespace std;
int main(){
int id, numInt, numProc, i;
double suma;
cin >> id >> numInt >> numProc;
suma = 0;
for (i = id; i < numInt; i += numProc){
suma += (4 / ((1 + (((i + 0.5)/numInt)*((i + 0.5)/numInt)))));
}
suma = suma / numInt;
//Haciendo que cada uno dure distintos tiempos
//srand(time(NULL));
//int espera = 1+(int) (10.0*rand()/(RAND_MAX+1.0)) + id;
//sleep(espera);
cout.precision(10);
cout << suma << endl << flush;
}
El proceso padre enviará los datos de la tarea a los hijos y recibirá
los resultados usando los manejadores proveídos por open2.
El número de tareas
Use comunicaciones sin buffers y sin bloqueo.
Utilice IO::Select en el procesador 0
para determinar que canales están listos para
recibir. Perturbe artificialmente los tiempos
de espera de cada proceso con sleep
y observe que sucede.
Casiano Rodríguez León
