

Sig: SSH: Secure Shell Sup: Pipes con nombre Ant: Práctica: Pipes con Nombre.
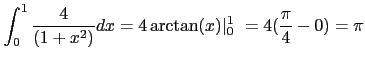
Esta integral puede aproximarse por la suma:
lhp@nereida:~/Lperl/src/perl_networking/ch2$ cat -n pi.c
1 #include <stdio.h>
2 #include <stdlib.h>
3
4 main(int argc, char **argv) {
5 int id, N, np, i;
6 double sum, left;
7
8 if (argc != 4) {
9 printf("Uso:\n%s id N np\n",argv[0]);
10 exit(1);
11 }
12 id = atoi(argv[1]);
13 N = atoi(argv[2]);
14 np = atoi(argv[3]);
15 for(i=id, sum = 0; i<N; i+=np) {
16 double x = (i + 0.5)/N;
17 sum += 4 / (1 + x*x);
18 }
19 sum /= N;
20 if (id) {
21 scanf("%lf", &left);
22 sum += left;
23 }
24 fflush(stdout);
25 printf("%lf\n", sum);
26 // fprintf(stderr, "[%d] %lf\n", id, sum);
27 }
Es posible establecer un pipe entre diversas réplicas de este programa
para calcular una aproximación a ![]() . Veamos un ejemplo
de ejecución en pipe:
. Veamos un ejemplo
de ejecución en pipe:
lhp@nereida:~/Lperl/src/perl_networking/ch2$ gcc pi.c -o pi
lhp@nereida:~/Lperl/src/perl_networking/ch2$ time pi 0 1000000 4 | pi 1 1000000 4 | \
pi 2 1000000 4 | pi 3 1000000 4
3.141592
real 0m0.026s
user 0m0.070s
sys 0m0.010s
En secuencia:
lhp@nereida:~/Lperl/src/perl_networking/ch2$ time \
(pi 0 1000000 4; echo 0 | pi 1 1000000 4 ; echo 0 | pi 2 1000000 4 ;\
echo 0 | pi 3 1000000 4)
0.785399
0.785398
0.785398
0.785397
real 0m0.042s
user 0m0.040s
sys 0m0.000s
Usando pipes con nombres:
lhp@nereida:~/Lperl/src/perl_networking/ch2$ mkfifo f0 f1 f2
lhp@nereida:~/Lperl/src/perl_networking/ch2$ time ((pi 0 1000000 4 >f0 &);\
(pi 1 1000000 4 <f0 >f1 &); (pi 2 1000000 4 <f1 >f2 &); (pi 3 1000000 4 <f2))
3.141592
real 0m0.025s
user 0m0.020s
sys 0m0.010s
Escriba un programa Perl que lee/evalúa un fichero de
configuración describiendo una secuencia de comandos a ejecutar.
Según la opción en la línea de argumentos -p|-n|-s
el programa ejecuta los comandos en pipe, pipe con nombres
o en secuencia.
Escriba en un módulo UnixProcess::Composition::Simple con funciones genéricas que
retornen la cadena unix que describe la composición
de los comandos en secuencia, en pipe y en pipe con nombre.
Sigue un ejemplo de lo que podría ser el código de la función
que implanta los pipes ordinarios:
pp2@nereida:~/src/perl/pipesconnombre$ sed -ne '63,73p' pi_pipenamed_cas.pl | cat -n
1 sub unixpipe {
2 my @commands = @_;
3
4 my $lastproc = $#commands;
5 my @cmds = map { "$commands[$_] |" } 0..$lastproc;
6 our ($a, $b);
7 my $cmds = reduce { "$a$b" } @cmds;
8 chop($cmds); # Supress final |
9
10 return $cmds;
11 }
La función hace uso de reduce que se encuentra en List::Util .
Otra función que puede serle útil al escribir la práctica
es all en List::MoreUtils :
die "All args must be numbers" unless all { /\d+/ and $_ > 0 } @ARGV;
Para llamar a la función unixpipe necesita preparar los comandos
para que incluyan a los argumentos.
Para el programa de cálculo de
@commands = map { "$command $_ $nblocks $nprocs" } 0..$nprocs-1;
my $pipe = unixpipe(@commands);
system $pipe or die "Can't execute $pipe";
Utilice IPC::Run3 para la ejecución si está instalado.
Compare los tiempos obtenidos
usando la función timethese del módulo Benchmark para las comparaciones.
Cuando entregue la práctica acompañela de todos los ficheros necesarios.
Casiano Rodríguez León
