Definimos el lenguaje árbol homogéneo ![]() sobre
sobre ![]() inductivamente:
inductivamente:
- Todos los elementos de aridad 0 están en
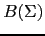 :
:
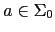 implica
implica
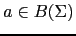
- Si
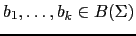 y
y
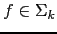 es un elemento
es un elemento
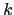 -ario, entonces
-ario, entonces
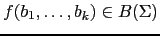


Definimos el lenguaje árbol homogéneo ![]() sobre
sobre ![]() inductivamente:
inductivamente:
![]()
|
|
|
|
|
|
|
|
Observe que los elementos en ![]() no necesariamente son
árboles ``correctos''. Por ejemplo, el árbol
no necesariamente son
árboles ``correctos''. Por ejemplo, el árbol
![]() es un elemento de
es un elemento de ![]() .
.
Si
![]() es una producción y
es una producción y ![]() es de tipo
es de tipo
![]() ,
diremos que la producción
,
diremos que la producción ![]() es de tipo
es de tipo
![]() .
.
La producción
![]() es del tipo
es del tipo
![]() .
.
Informalmente, el lenguaje generado por ![]() se obtiene realizando sustituciones
sucesivas (derivando) desde el símbolo de arranque hasta producir un
árbol cuyos nodos estén etiquetados con elementos de
se obtiene realizando sustituciones
sucesivas (derivando) desde el símbolo de arranque hasta producir un
árbol cuyos nodos estén etiquetados con elementos de ![]() . Debería ser claro
que, en este ejemplo,
. Debería ser claro
que, en este ejemplo, ![]() es el conjunto de las listas en
es el conjunto de las listas en ![]() , incluyendo la lista vacía:
, incluyendo la lista vacía:
Cuando hablamos del AAA producido por un analizador sintáctico, estamos en realidad hablando de un lenguaje árbol cuya definición precisa debe hacerse a través de una gramática árbol regular. Mediante las gramáticas árbol regulares disponemos de un mecanismo para describir formalmente el lenguaje de los AAA que producirá el analizador sintáctico para las sentencias Tutu.
|
|
|
|
|
|
|
|
|
|
|
|
||
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
Entonces el lenguaje ![]() contiene árboles
como el siguiente:
contiene árboles
como el siguiente:
|
|
|
||
| |
|||
| |
|
||
| |
|||
| |
|
||
| |
|||
| |
|||
| |
|||
| |
|||
| |
El cual podría corresponderse con una sentencia como
a = b + 4 * c.
El lenguaje de árboles descrito por esta gramática árbol es el lenguaje de los AAA de las sentencias de Tutu.
Intente dar una definición formal del concepto de árbol de análisis sintáctico asociado con una derivación en una gramática árbol
|
|
|
||
| |
|||
| |
|
||
| |
|||
| |
|
||
| |
|||
| |
|||
| |
|||
| |
|||
| |
Calcule los subárboles
![]() ,
,
![]() ,
,
![]() y
y
![]() .
.

