















Sig: Selección de Código y
Sup: Transformaciones Árbol con Parse::Eyapp
Ant: Transformaciones Árbol con Parse::Eyapp
Err: Si hallas una errata ...
Árbol de Análisis Abstracto
Un árbol de análisis abstracto (denotado AAA, en
inglés abstract syntax tree o AST)
porta la misma información que
el árbol de análisis sintáctico pero de forma mas condensada, eliminándose
terminales y producciones que no aportan información.
Definimos el lenguaje árbol homogéneo 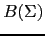 sobre
sobre 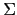 inductivamente:
inductivamente:
- Todos los elementos de aridad 0 están en
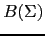 :
:
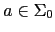 implica
implica
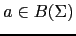
- Si
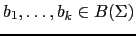 y
y
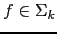 es un elemento
es un elemento
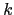 -ario, entonces
-ario, entonces
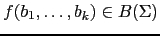
Los elementos de 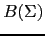 se llaman árboles o términos.
se llaman árboles o términos.
Ejemplo 10.1.2
Una versión simplificada del alfabeto con aridad en el que estan basados
los árboles construidos por el compilador de Tutu es:
Observe que los elementos en 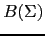 no necesariamente son
árboles ``correctos''. Por ejemplo, el árbol
no necesariamente son
árboles ``correctos''. Por ejemplo, el árbol
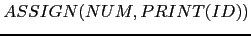 es un elemento de
es un elemento de 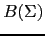 .
.
Definición 10.1.5
Se define el lenguaje árbol generado por una gramática
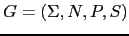 como el lenguaje
como el lenguaje
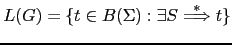 .
.
Ejercicio 10.1.1
Construya una derivación para el árbol
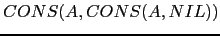 .
¿De que tipo es el árbol
.
¿De que tipo es el árbol
 ?.
?.
Cuando hablamos del AAA producido por un analizador sintáctico,
estamos en realidad hablando de un lenguaje árbol cuya definición
precisa debe hacerse a través de una gramática
árbol regular.
Mediante las gramáticas árbol regulares disponemos de un mecanismo para
describir formalmente el lenguaje de los
AAA que producirá el analizador sintáctico
para las sentencias Tutu.
Ejemplo 10.1.4
Sea
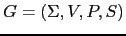 con
con
y las producciones:
Entonces el lenguaje 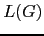 contiene árboles
como el siguiente:
contiene árboles
como el siguiente:
El cual podría corresponderse con una sentencia como
a = b + 4 * c.
El lenguaje de árboles descrito por esta gramática árbol
es el lenguaje de los AAA de las sentencias de Tutu.
Ejercicio 10.1.2
Redefina el concepto de árbol de análisis concreto dado
en la definición 8.1.7 utilizando el
concepto de gramática árbol. Con mas precisión,
dada una gramática
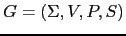 defina una gramática
árbol
defina una gramática
árbol
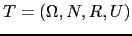 tal que
tal que 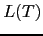 sea el lenguaje
de los árboles concretos de
sea el lenguaje
de los árboles concretos de 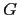 . Puesto que las partes
derechas de las reglas de producción de
. Puesto que las partes
derechas de las reglas de producción de 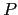 pueden ser
de distinta longitud, existe un problema con
la aricidad de los elementos de
pueden ser
de distinta longitud, existe un problema con
la aricidad de los elementos de 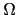 . Discuta posibles
soluciones.
. Discuta posibles
soluciones.
Ejercicio 10.1.3
¿Cómo son los árboles sintácticos en las derivaciones árbol?
Dibuje varios árboles sintácticos para las gramáticas
introducidas en los ejemplos
4.9.3
y 4.9.4.
Intente dar una definición formal del concepto de árbol de análisis
sintáctico asociado con una derivación en una gramática árbol
Definición 10.1.6
La notación de Dewey es una forma de especificar los subárboles
de un árbol
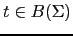 . La notación sigue el mismo
esquema que la numeración de secciones en un texto:
es una palabra formada por números separados
por puntos. Así t/2.1.3
denota al tercer hijo del primer hijo del segundo hijo
del árbol
. La notación sigue el mismo
esquema que la numeración de secciones en un texto:
es una palabra formada por números separados
por puntos. Así t/2.1.3
denota al tercer hijo del primer hijo del segundo hijo
del árbol 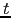 .
La definición formal sería:
.
La definición formal sería:
-
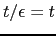
- Si
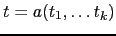 y
y
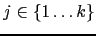 y
y 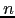 es una
cadena de números y puntos, se define
inductivamente el subárbol
es una
cadena de números y puntos, se define
inductivamente el subárbol 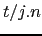 como el subárbol
como el subárbol 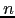 -ésimo del
-ésimo del
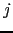 -ésimo subárbol de
-ésimo subárbol de 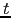 . Esto es:
. Esto es:
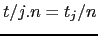
El método descendant de los objetos Parse::Eyapp::Node
descrito en la sección
8.22
puede verse como una implantación de la notación de Dewey.
Subsecciones
















Sig: Selección de Código y
Sup: Transformaciones Árbol con Parse::Eyapp
Ant: Transformaciones Árbol con Parse::Eyapp
Err: Si hallas una errata ...
Casiano Rodríguez León
2012-05-22


![]()
![]() no necesariamente son
árboles ``correctos''. Por ejemplo, el árbol
no necesariamente son
árboles ``correctos''. Por ejemplo, el árbol
![]() es un elemento de
es un elemento de ![]() .
.![]() es una producción y
es una producción y ![]() es de tipo
es de tipo
![]() ,
diremos que la producción
,
diremos que la producción ![]() es de tipo
es de tipo
![]() .
.![]() es del tipo
es del tipo
![]() .
.
![]() se obtiene realizando sustituciones
sucesivas (derivando) desde el símbolo de arranque hasta producir un
árbol cuyos nodos estén etiquetados con elementos de
se obtiene realizando sustituciones
sucesivas (derivando) desde el símbolo de arranque hasta producir un
árbol cuyos nodos estén etiquetados con elementos de ![]() .
En este ejemplo,
.
En este ejemplo, ![]() es el conjunto de arboles de la forma:
es el conjunto de arboles de la forma:
![]() contiene árboles
como el siguiente:
contiene árboles
como el siguiente:
![]() ,
,
![]() ,
,
![]() y
y
![]() .
.
