Resumen Tema 1
Tema 1. Integral de Riemann múltiple
 |
Nos ocuparemos a continuación de definir y estudiar la integral múltiple en el sentido de Riemann. La teoría será desarrollada fundamentalmente en el plano, pero se puede trasladar sin dificultad a dimensiones superiores. Comenzamos definiendo la integral de las llamadas funciones escalonadas sobre rectángulos, para luego considerar funciones y dominios más generales. El teorema de Lebesgue caracterizará las funciones integrables como aquellas cuyo conjunto de discontinuidades tiene medida nula.
Una vez definida la integral, interesa encontrar herramientas para calcularla. Entre ellas se encuentran:
El tema concluye con el estudio de las integrales impropias y paramétricas múltiples. |
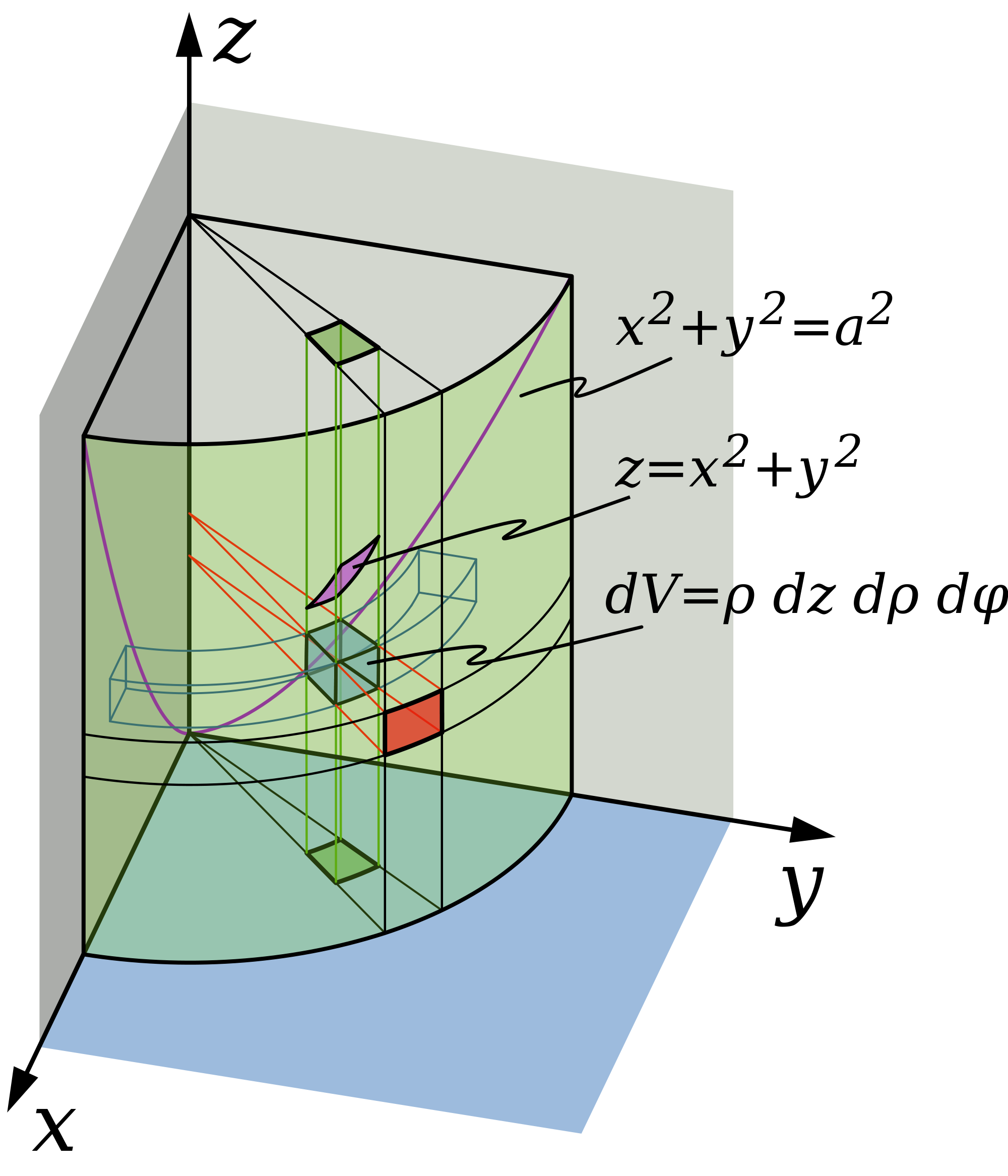
| Fuente de la imagen: Wikimedia Commons |
|
Última modificación: martes, 25 de junio de 2013, 09:36